|
Tadeusz Sozański: Voting Games |
Files 2004-2006 (in Polish) (in Polish) (in Polish) 2007-2010 (in Polish) (in Polish) (in Polish) 2014 |
You can read below a report on my activities in a research area which can be called mathematical theory of voting systems and its applications. Having entered the area in 2004, I have placed until today in my Internet niche my comments or analyses, which I wrote down piece by piece with the intention to keep pace with the course of EU institutional decisions and ongoing discussion of academic experts. Sometimes, however, I re-edited the notes which had been added immediately after important events in the world of politics (EU summits) or in the academia (conferences). Thus, this part of my website departs from a regular blog, although the collection of notes is arranged chronologically. Click here to jump to the final section of my story. I added this section 8 months after there appeared in print my latest and probably the last paper in the field. Tadeusz Sozański, November 15, 2015 ----------- My interest in voting games has to do with my earlier work on n-person characteristic function form games associated with exchange networks (the topic of Chapter 5 of my book The Mathematics of Exchange Networks, in process; see Exchange Networks). Niza o muerte My first paper (Niza o muerte. On the use of game theory for politics; in Polish) provides a moderately technical comparative analysis of power distributions generated by two voting systems for the EU council: the one established by the Nice Treaty (2001) and the other proposed in the EU Constitution Draft. The article appeared January 28, 2004 in Cracow's largest daily Dziennik Polski, The text was a little trimmed by the editor without consulting the author. The original version with minor corrections is available here in pdf file (Niza.pdf). POWERIND To join the debate on EU voting games as an independent expert, I wrote a Quick Basic program named POWERIND which calculates few indices of voting power for the Nice Treaty voting game and other games of the kind. The latest version (April 2004) of my program is offered free to scientists, students, teachers, government officials or experts, politicians and anyone else interested in measurement of voting power. POWERIND can be applied to by far more voting games than those designed to be played by the EU Council, yet the number of players may not exceed 27 (the number of EU member states after the next enlargement). Here are the main features of the program:
● One can analyze not only a single weighted voting game but a double or triple majority game, obtained by combining 2 or 3 such games. One of them can be a one voter – one vote game, the other is based on an arbitrary allocation of votes like that given in the Nice Treaty, and the third game uses relative weights which add up to 1000 and are obtained from absolute weights. The latter weights (which can be the populations of EU member states) along with votes assigned to players by the user are read from an input file.
● Apart from overall and by-players coalition statistics and game efficiency (relative frequency of winning coalitions), the program computes 4 most often used normalized relative power indices: the Banzhaf-Coleman, Shapley-Shubik, Johnston, and Deegan-Packel, 2 absolute power indices (Banzhaf-Penrose, Coleman’ s Preventive Power Index).
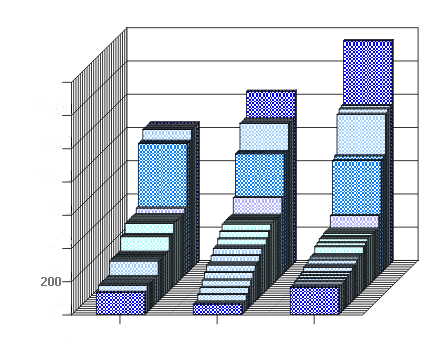
● Bar-chart graphic illustration of power distributions is displayed on screen, yet it can’t be printed. Text mode output is saved to an ascii file. The instructions on how to use POWERIND preceded by an introduction to the mathematical theory of voting games, and followed by an informal story are available here since April 22, 2004 as a pdf file (Powerind.pdf). To obtain POWERIND, send a request to my email address ussozans@cyf-kr.edu.pl Put “POWERIND” in the Subject: field in the header of your letter. If you are going to publish results obtained by means of my program, place a proper reference in your paper (T. Sozański. POWERIND. April 2004. Http://www.cyf-kr.edu.pl/~ussozans/). Note (November 2015). POWERIND does not work under Windows 7 or later (to run the program you need Windows XP or earlier). Which game to choose for the EU Council? Following my newspaper publication, I was invited by the Institute of Strategic Studies (a Polish NGO) to take part in a public debate on EU decision making rules. The conference, held in Cracow March 29, 2004, gave an opportunity to Polish specialists in mathematical social sciences to present their analyses before general audience and guests representing the Ministry of Foreign Affairs. The organizers encouraged the panelists to analyze the voting system designed for the EU Council by W. Słomczyński and K. Życzkowski (Faculty of Mathematics and Physics, Jagiellonian University). Their first article appeared January 30, 2004 in a leading nationwide daily Rzeczpospolita To settle the controversy, the authors proposed a single weighted voting game with Penrose square root weights (see D.S. Felsenthal, M. Machover. The Measurement of Voting Power. 1998, section 3.4). In their paper, presented at the beginning of the Cracow conference, Słomczyński and Życzkowski provided arguments for setting the quota for this game to 62% of the total amount of votes (hence they labeled P-62 their voting game). An English translation of this paper (“Zasady głosowania w Radzie UE: analiza matematyczna”. Międzynarodowy Przegląd Polityczny 7, 2004: 18-39) is available from the authors. The aim of my paper presentation (Which game to choose? The search for an acceptable voting system for the EU Council) was to compare the P-62 game with other games selected (upon the criterion of sufficiently high efficiency and moderate power inequality) from a two-parameter family of double majority games constructed by combining a 25-person one voter - one vote game with a quota varying from 13 to 18 with a game with relative populations weights and quota ranging from 55% to 80% of the total population of EU-25. The 13/600 game (chosen by the authors of the EU Constitution draft) failed to be accepted at the Brussels summit in December 2003 due to the objections raised by Poland and Spain. The first incomplete draft of an extended version of my conference paper with further results obtained with the help of POWERIND appeared April 22, 2004 on my homepage. ● As I consider P-62 to be the best of all compromise solutions I joined the international group of specialists in voting theory who have supported P-62 in the Letter to the Governments of the EU Member States (the letter I received from the initiators is available here in a pdf file (Letter.pdf). The P-62 voting system is worth implementation not only for its virtues appreciated by mathematicians. It can be advocated as well as a solution that should satisfy both the defenders of the Nice Treaty and the supporters of the EU Constitution. To see that P-62 is, in fact, a compromise between the two, just look at the visualization of three power distributions (voting power being measured by the Banzhaf index).
The three barcharts illustrate the voting power of 25 EU member states in the following voting games (.2 or 2.00% is written as 200) :
● the modified Nice Treaty game (left) in which 13 member states (the minimum majority in a one voter - one vote 25-person game) and 60% of the total amount of Nice votes are required for a coalition to be winning
● the EU Constitution game (right) in which 13 states and 60% of the total population are decision thresholds.
● the P-62 game (middle) with a threshold of 62% of the total number of votes under a different allocation of 321 votes among 25 states which is obtained by assigning to each country the number of votes proportional to the square root of its population. Under P-62, the EU population structure is mapped into the Union’s institutional system as postulated by the Convention, but the mapping proposed by the scientists is more democratic, since every citizen the EU, regardless of how large is his or her national state, is granted the same power to affect EU decisions. Unlike other proposals obtained by tinkering with quotas of two component games, the square root solution has an additional virtue of being derived from a mathematical model. The original Nice Treaty voting system can been corrected by removing the population threshold and lowering the quota for the game with “political” weights to the level of 60% “inspired” by the relative population quota chosen by the Convention. Such a correction entails a significant improvement on efficiency (20.4% which is nearly as high as 22.5% obtained for the Constitution game). I don’t know the position currently defended by the Polish government. I like most the modified Nice Treaty game which has a sufficiently high efficiency so that the objection that Poland and Spain hold fast to the solution that helps them block EU decisions is no longer valid. What Poland and Spain would like to save and what the Convention found untenable in the Nice Treaty is a system of “political” weights constructed with a clear intention to extend the parity principle from 4 to 6 largest EU member states. However, the four largest states have decided on no longer applying even to themselves the principle considered the cornerstone of political balance in Europe for 3 decades. In such circumstances, the remaining EU members have no choice but to acknowledge new political reality and to seek a compromise based on an alternative political principle, that of democratic representation of the future European nation. I recommend to Polish government to support the P-62 voting system which is more consistent with this principle than any “double majority system” including the one which has recently popped up in the mass media, namely, the proposal of raising the two thresholds from 13 to 14 in the one state - one vote game and from 60% to 65% in the population game. The 14/650 game is a bit less efficient than P-62 (13.6% vs. 16.9%). It induces almost identical power inequality as P-62, both games being less controversial in this respect than the 13/600 game. Following the failure of the Brussels summit (December 2003) the supporters of the EU Constitution have realized that the game chosen by the Convention is but one of many plausible solutions and conceded to consider other games of the kind. Before the conference which took place in Cracow at the end of March 2004, Polish newspapers pointed to 55% (which translates to 14 states) and 55% as two thresholds then considered as a possible compromise. The 14/550 game has a greater efficiency (23.0%) than P-62, yet it flattens the power distribution too much to be approved of by the largest EU members. I suspect that it is the reason for which this solution has been replaced with14/650. What happened June 18, 2004 in Brussels? [the text which I placed under such a title June 23, 2004, was replaced, December 21, 2004, with the following note based on further analyses] I came to know what happened June 18, 2004 late evening that day from the Polish public TV news. The following day I wrote an article on the distribution of power in EU-25 and emailed it to Cracow’s daily Dziennik Polski. My analysis which appeared June 22 was based on an incorrect account of what the leaders of 25 states had actually agreed on, namely, the TV news failed to inform that the double majority with 55% of the EU members and 65% of the EU population should comprise at least 15 states. As a consequence, I analyzed the game 14/650 (55% of 25 equals 13.75) instead of 15/650. In addition, I did not know then that the article defining "qualified majority" had been supplemented with a clause on the minimum size of a "blocking minority." Here is the relevant passage from the final text of the EU Constitution, quoted from The EU Constitution – the reader-friendly edition by Jens-Peter Bonde. Nov 1, 2004. Http:/ www.euabc.com/upload/rfConstitution-en.pdf).
Article I-25: Definition of qualified majority within the European Council and the Council
1. A qualified majority shall be defined as at least 55% of the members of the Council, comprising at least fifteen of them and representing Member States comprising at least 65% of the population of the Union. A blocking minority must include at least four Council members, failing which the qualified majority shall be deemed attained. The aim of my paper which appeared in Dziennik Polski was to show how to choose a game that would satisfy all 25 EU members from among the set of all double majority games obtained by combining a one state - one vote game and a game with relative population weights.
● First, the set of potential solutions should be narrowed down by imposing certain conditions on acceptable games. I proposed two conditions: (1) the efficiency a voting game to be selected should be sufficiently high, say, no les than 10%; (2) the standard deviation of the Banzhaf index values should be neither too low nor too high; specifically, let it lie between 100 and 400 points (1 point = .0001).
● Both conditions are met by 9 out of 30 games with q1=13, 14, 15, 16, 17 and q2=550, 600, 650, 700, 750, 800.These 9 games are listed below (efficiency and standard deviation are given in brackets for each game) in the order of increasing standard deviation: 15/550 (15.8; 116), 15/600 (13.1; 160), 14/550 (23.0; 178), 15/650 (10.2; 208), 14/600 (18.2; 231), 13/550 (29.4; 258), 14/650 (13.6; 283), 13/600 (22.5; 315), 13/650 (16.1; 363). To further reduce the number of potential solutions, one can skip those at the ends of this sequence.
● Thus, we are left with 7 games from which the politicians could choose one so as make everybody as happy as possible with the compromise achieved. If each of 25 players agrees to accept the game such that his voting power lies half way between his worst-fear and best-hope value in the set of values obtained for the 7 games under consideration, then the 14/600 game should be selected for the EU Constitution. June 23, 2004, I placed on my web page the above summary of my paper and concluded that the largest EU members had won the tug of war. Actually, the 14/650 game lies to the right of the compromise game 14/600. However, in accordance with Article I-25.1 any winning coalition must have at least 15 members. Therefore, EU-25 is going to use the 15/650 game, more exactly, the game obtained by adding winning coalitions which are complements of 12 3-element "blocking minorities". Since the 15/650 game lies to the left of the center, 19 smaller countries should be more happy than the largest Six. In October 2004, I carried out further analyses to prepare illustrative material for the course on "Formal Models in Politics" which I began to teach for the first time in the current academic year. Meanwhile the treaty establishing the EU Constitution was signed in Rome October 29, 2004 and the official English text appeared in the Web. Being, at long last, sure of what to analyze, I wrote a Postscript to my article. The article's original version and the Postscript (actually a sizable paper) are now available here in one file Komprops.pdf. The first part of the Postscript shows the results of similar analyses now done for a family of double majority games with 27 players. By applying the same criteria (minimum efficiency, moderate power inequality), I arrived at the following 7 games: 16/600, 15/550, 16/650, 15/600, 14/550, 15/650, 14/600. The Shapley-Shubik index, used instead of the Banzhaf-Coleman index (see Tables1 and 2 in the Postscript where 27 states are listed in the order of decreasing population), yields a little different order: 15/550, 16/600, 14/550, 15/600, 16/650, 14/600, 15/650, yet in both sequences the same game15/600 lies in the middle so that the compromise does not depend on the choice of a voting power index. Under both most popular indices, the 15/650 game is most advantageous for the Big Four. Spain and Poland would benefit a bit more if the Convention game 14/600 were chosen and the Shapley-Shubik index were used to assess voting power. Both classical indices applied to the games based on relative populations weights give to Germany a considerable power advantage over France, UK, and Italy. In my first paper (Niza o muerte), I pointed to political interests of the Big Three as a plausible explanation of their consent to the proposition of the European Convention (in particular, France may have accepted the population weights which make Germany the strongest player as the only way to give more power to Franco-German coalition). I do not give up the "political" explanation, but now I tend to believe that there is another reason for which Germany's enormous voting power does not worry the three remaining big players, namely, I am almost sure that their experts have used a different method to assess the amount of voting power. My working hypothesis is that what the EU politicians and their consultants understand by voting power and what they wanted to maximize for their countries is, in fact, the blocking power, a special dimension of voting power which can be generally defined by the following statement. The blocking power of a player decreases with the number of other players needed to form a minimal blocking coalition and increases with the number of players from which the given player can choose partners for "small" minimal blocking coalitions. The second part of the Postscript is the first draft of a paper in which I'm going to draw a distinction between blocking and winning power, quantify the two concepts, and apply a new measure of blocking power to old (EU-15) and new EU games. The Banzhaf-like coefficient, available in the current version of POWERIND, cannot serve this purpose because it assumes identical values as the Banzhaf index for most voting games. December 21, 2004 (May 4, 2006, few minor changes were made to the above text, and the file whichg.pdf was removed - TS) 14 months later 14 months have lapsed since I placed the Postscript (see Komprops.pdf) on my homepage. Having edited the last note (dated December 21, 2004), I stopped working on a paper I planned to submit to a refereed international journal and thus close with a publication my excursion into the mathematical theory of voting games and its political applications. Similarly, the POWERIND program is not yet enriched with procedures for the calculation of new indices of blocking power. In the meantime the EU Constitution Treaty was rejected in referenda in France and the Netherlands to the Schadenfreude of the political forces which won the parliamentary and presidential election in Poland in Autumn 2005 and to the puzzlement of the postcommunists and their allies who were long in favor of continuing the ratification process in other countries, including Poland. The new government has voiced mild suggestions to start work from scratch on a new treaty, but its priority is now to enhance integration in the domains where it has already proved successful (the Prime Minister has recently come up with a reasonable idea of "common security policy" concerning oil and gas supplies). In these circumstances, the square root voting system which, in fact, fits the "United States of Europe" rather than the union of states, is highly unlikely to win support of two currently strongest parties, "Law and Justice" and "Civic Platform" (the ruling party and the opposition, both with Solidarity roots). As regards myself, I still consider P-62 the best of all voting games with weights functionally related to member states' populations, yet I believe that one should return to the weights reflecting a negotiated balance of power and part with the idea to connect decision rules with demographic structure. I would be glad if you let me know of any new insights or formal approaches to voting power which were proposed by mathematical political scientists since June 2004 until present. As I was busy with other problems, I had too little time to study the literature or browse through the cyberspace. My current attempt to resume work on blocking power has to do with an invitation to take part in the symposium which will be held in Cracow in April, 2006 (see http://www.science24.com/event/fens2006/). The organizers are a group of Polish physicists who want to bridge the gap between their discipline and the economic and social sciences. The conference will cover a wide range of topics, including game theory applications. The abstract (in English) of my paper On Winning and Blocking Power in Voting Games is given here in the pdf file (Wbabs.pdf). February 23, 2006 The file winblock.pdf containing my conference presentation (in Polish, April 22, 2006) is available here since May 4, 2006. May 4, 2006 Spring 2007: my adventure with voting games goes on In March 2007, I learnt from the daily press that the Polish government (now with Jarosław Kaczyński as Prime Minister) had been trying to gain support from other EU member states for replacing - in a new voting system that is to be designed for the EU Council - linear population weights with square root weights. Contrary to the prediction that I stated in my previous note, the square root system has been backed both by the Civic Platform and the ruling Law and Justice. Many people, including myself, who have divided their sympathy between these two parties now fighting with each other, welcome the good news that the two wings, liberal and conservative of the post-Solidarity camp, albeit they failed to form a grand coalition government, are at least able to cooperate in foreign affairs. A new independent nationwide daily Dziennik, which has been addressing this category of voters, published, March 13, 2007, an article defending the square root system. The arguments raised by the academic proponents of this solution were repeated once again by Jacek Saryusz-Wolski, an experienced politician representing the Civic Platform in the European Parliament (he is now the Chairman of the EP Foreign Affairs Committee). I know and accept these arguments, yet I understand why the EU politicians still remain unconvinced. The reason is that they don't use classical coefficients to calculate voting power so that they can't appreciate Penrose's theory. As regards myself, I have long ignored the fact that the politicians are interested in assessing blocking power as measured by the number of small "blocking minorities" that a player can form with other players. Now I believe that mathematical theory of voting games should be reoriented so as to come closer to political practice. Unfortunately, I have again been too busy with other work so that I must put off for later what I should do as a scientist, that is, write a scholarly paper and submit it to a refereed international journal. After the conference, I placed on my web page the first draft of such a paper (On Winning and Blocking Power in Voting Games) but it is still available in Polish only. Being sure of practical implications of my new analyses, I also sent the file to Polish Ministry of Foreign Affairs and handed the printed copy to the EU Commission Vice-President Margot Wallström whom I met at the lecture she had in June 2006 at the Jagiellonian University. At the conference which took place a year ago, I presented an analysis of blocking power in the Nice treaty game and Constitution treaty game. I defined regularity of a blocking structure by the condition that the order of players with respect to the number of minimal blocking coalitions containing a given player, for any small coalition size, reproduces the order of players with respect to their weights. I found that the game used in EU-15 has a regular blocking structure, whereas the Nice game and the Constitution game fail to meet this requirement. Hence the main reason for rejecting these games is that they are badly constructed. In the last section of my conference paper, I stated the hypothesis that square root weights generate regular blocking structure, yet I had not done the calculations to verify my hunch until Saryusz-Wolski's article spurred me to resume research. Now I can tell you that the square root system with a proper quota has the required property. Thus, we get another argument for its implementation, the argument that should appeal to the EU politicians. In April 2007, I wrote a short paper (in Polish) in which I analyzed the voting system with square root weights given in Saryusz-Wolski's article. I sent this paper to Cracow's daiIy Dziennik Polski and to Dziennik (no reply has come until today from their editors). I also sent it to Professors Słomczyński and Życzkowski. Professor Słomczyński suggested that I should repeat the analysis with the most recent population data, now being used by the German presidency (first half of 2007). Having done the calculations with the new data, I added a postscript to my article and placed both on my web page in one file sqrtblck.pdf which I sent to my colleagues from the Jagiellonian University, Saryusz-Wolski, and few other politicians. As a consequence, Konrad Szymański, a Member of European Parliament (representing there the "Law and Justice" party) and the Editor of Polish political bimonthly Międzynarodowy Przegląd Polityczny (International Political Review) invited me to publish a paper in his journal. Having used the paper for Dziennik Polski with the postscript as a source, I wrote a new paper (its title is: "On Square Root and Blocking Minorities: A New Analysis of Voting Systems for the EU Council") and sent it (May 11, 2007) to the Editor of the journal in question (see www.mpp.org.pl; in Polish). The paper (tsmpp18.pdf) is also available on my website (old file sqrtblck.pdf was removed). I did old and new calculations using the new version of my POWERIND program which is now endowed with a procedure for counting small size blocking coalitions. Unfortunately, the new version is not yet ready for free distribution because some output display procedures still have to be written. May 16, 2007 I learnt that Professors J.M. Bilbao and K. Życzkowski had been invited to present their analysis of the square root voting system at a conference "Rules for decision-making in the Council - which way forward?" The one-day session has been scheduled for May 23, 2007. It will be held in Brussels in European Policy Center (www.epc.edu). May 19, 2007, I emailed an open letter to my Colleagues with further arguments for the square root voting system. My letter (see jmbkzltr.pdf) is, in fact, a short paper based on the above mentioned paper in Polish. You will find there a summary of the main results concerning blocking structures in few voting systems designed for the EU Council. The last section gives some directions on how to solve the perplexing problem of designing mathematically reasonable and politically acceptable "rules for decision-making in the Council". April 27, May 11, 20, June 3, 24, 2007 The battle for the square root The battle was lost, but did the Polish government really want to win it? Had the Prime Minister Kaczyński actually intended to convince Chancellor Merkel to accept the square root system, he wouldn't have said "we are ready to die for the square root system". He would rather reassure the Germans that they would not necessarily lose too much of their voting power granted by the Constitution system if the population weights were replaced by the square root weights. Indeed, the square root weights allow for designing many weighted voting games with blocking structures satisfying political aspirations of particular groups of EU-27 member states. In my paper for Międzynarodowy Przegląd Polityczny (see the author's version in file tsmpp18.pdf now with a postcript), I have shown how to do this by varying quota. For example, it is easy to construct a square root voting system which could be called the "German game" as it is similar to the Constitution "double majority system" without the clause which stipulates that "a blocking minority must include at least four Council members" (the clause was added to lessen Germany's advantage over France, UK and Italy). Soon after my paper appeared in print (at the beginning of June), Professor Słomczyński noticed a flaw in my analysis of the blocking structure of the Constitution game. I corrected my error in the Appendix that I added to my last year conference paper (see pp. 39-43 in file winblock.pdf, in Polish). An appropriate explanation and correction has also been appended to the letter to Professors Bilbao and Życzkowski (jmbkzltr.pdf). You will find there the correct distribution of blocking fours in the Constitution game as well as the analysis of the game with quota 255 and integer square root weights which sum up to 345 (like the Nice treaty weights). The two games have similar distributions of blocking fours, but in the latter game Germany's advantage over France is a bit smaller. President Sarkozy would probably like this game if his advisors showed to him my analysis. Certainly, q=213 (the "Polish quota" which is obtained as the integer counterpart of the 61.6% relative quota proposed by Słomczyński and Życzkowski), q=246 (the quota for the "German game"), and q=255 (the quota for the "French game") are not the only plausible values that should be considered, were the "square root method" for constructing voting games admitted to the negotiation table. I don't know if Polish negotiators tried to dispel the fears of their German colleagues that their Vaterland would be verloren if they accepted the "compromise" proposed by two Professoren from the Jagiellonian University? Polish top political leaders and the media have occasionally quoted the opinions of the scientists and allowed them to speak to the public. Following my publication in MPP, I was invited by Channel 3 of the Polish Radio to take part as mathematical expert in the debate which took place on the air June 21 in the evening during the Brussels meeting. When my turn came, I managed to secure some 10 minutes of the program for a "lecture" on the importance of blocking coalitions. When I was asked for an interview by Dziennik, I offered to this daily another paper already written in the form of a dialog between a Journalist and a Mathematician. I wrote the dialog, following the suggestion of Dr. Trzaskowski (an advisor of EP member Saryusz-Wolski) to produce a less sophisticated text for the mass audience. I have few tentative explanations of why Dziennik refused to publish my paper I have just placed on my web page (dialog.pdf). One of these explanations has to do with the strategy which was probably adopted by the Law and Justice government. The Kaczyński Brothers had to show their resolve in defending national interests so they said that Poland would never accept the Constitution voting system. But they also had to show their will to achieve a compromise. They made the square root system (originally supported only by the Civic Platform) the official Polish proposal. However, it seems to me that the government was too little interested in getting its EU partners involved in a matter-of-fact discussion. The role of scientists in the political debate was too limited as if the Polish government deliberately refrained from using their arguments to convince the Germans to give up their prejudice against the scientific approach to designing voting system. The Prime Minister took pains to make his EU partners believe that Poland stood by the square root system as the most preferred option. Actually, he and most of his compatriots did not cease to consider the Nice voting system as the best solution for Poland. If so, the task for Polish negotiators became to persuade their partners that the only way to save Europe from the demonized new system is to stay for as long as possible with the already familiar Nice system. Thus, the defeat of the scientists became the victory of Polish diplomacy. The Germans should also be happy with the Nice system as it gives them the right to block any decision with 2 out of 3 largest countries which cannot alone block Germany's initiative because the coalition {France, UK, Italy} has only 36.9% of EU total population. The third component (the 62% population majority) of the Nice game is usually ignored in Poland where political elites and the grass roots still repeat Niza o muerte and are happy with 27 votes assigned to Semi-Big Two so close to 29 votes for the Big Four. June 25, 2007 This is to inform that my second paper (in Polish) appeared in Międzynarodowy Przegląd Polityczny, 2007, no. 3 (19). It is also available here in file Tsmpp19.pdf September 27, 2007 International Workshop in Natolin Following my first publication in MPP I was invited to present a paper at the International Workshop "The Distribution of Power and Voting Procedures in the European Union". The Workshop was held October 12-13, 2007 in Warsaw at European Center Natolin. Papers were presented by scholars from Britain, Czech Republic, Finland, France, Germany, Italy, Netherlands, Poland, Spain and Sweden. The conference program is given in file workshop.pdf. Most of the authors appear in the picture displayed below.
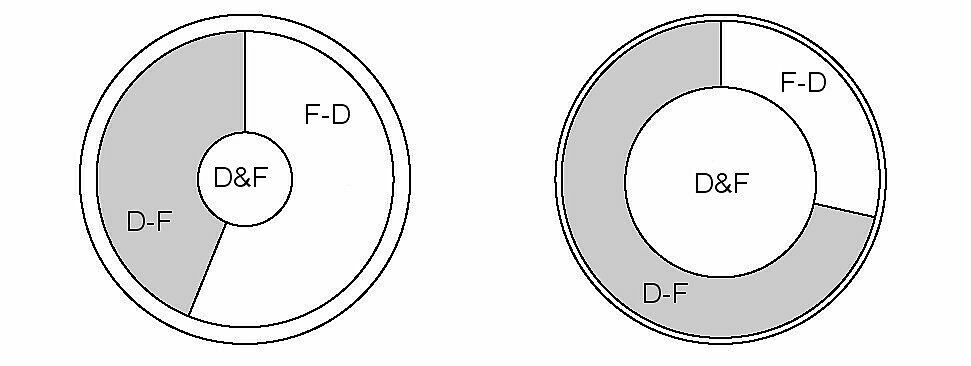
The organizers from the Natolin center did all in order that the participants remember their hospitality. Special thanks are due to Professor Karol Życzkowski. The workshop he organized as scientific coordinator gave the international group of experts an opportunity to confirm their willingness to help EU political elites in reforming decision procedures according to the principle Plus ratio quam vis (reason matters more than force, the Jagiellonian University motto). The paper I presented and submitted for publication in the Proceedings of the Natolin workshop was written not only for fellow mathematicians doing research on voting games. As it involves only elementary mathematics, it should be intelligible for politicians too. December 22, 2007 (the last paragraph of the above section and the section that follows, dated December 2008, were reedited in November 2015). After a year of uncertain prospects for publishing the Proceedings the Natolin Center informed the contributors that a British publishing house had agreed on publishing a book with the papers submitted by the Workshop participants. However, we learnt that the length of any paper to be included in the book may not exceed 7000 words. Since my contribution was twice as long, I decided to resubmit to the Natolin Center an abridged version, and try to get the paper published, in its original shape and content, in a journal in mathematical political science (in December 2007, I removed the original full text of my paper from my website). December 15, 2008 "Institutional Design and Voting Power in the European Union" Such is the final title of the collection of papers presented at the Natolin workshop, edited by Marek A. Cichocki (Natolin European Center) and Karol Życzkowski (Jagiellonian University; http://chaos.if.uj.edu.pl/~karol/)), and published in a book by Ashgate Publishing Ltd. The book (see more info in the file Ashgate.pdf I downloaded from the website of the publisher) appeared in October 2010 to the great satisfaction of the contributors who had to wait 3 years for seeing their papers in print. What I find most important and most novel in my contribution ("The Blocking Power in Voting Systems", Chapter 5, pp. 75-92) is the elaboration of a non-classical approach to voting power and the use of the concept of blocking power to characterize bilateral relations in a voting assembly. The analysis is illustrated with the following picture
which shows that France (F) will lose its moderate advantage over Germany (D) after the transition from the Nice to the Lisbon voting system. The latter gives D an enormous blocking power advantage over F. To learn more about the quantities displayed by means of the above pictures, have a look at pp. 88-89 of my paper in the book in question. (there followed a section that was removed in November 2015)
October 12, 2010 My next and latest paper on voting games (Decyzje22.pdf) appeared 4 years after my previous paper (the one in the 2010 book, see the note given above). Having come back with the habilitation degree (2014) from my excursion into pure humanities (see Miscellanea), I revisited the research area in which my doings are reported here. My old plan to get published in a journal my earlier results (those skipped to abridge my contribution for the 2010 book) succeeded in accepting my paper for publication in the 2014/2 issue of Decyzje (http://decyzje.pl), a Polish biannual which deals with decision theory and its applications. Unfortunately, although I count this paper among my major achievements in mathematical social science (see Publications), I can't call it my big academic success because an author scores - under the state system of parametric evaluation of publications - only 6 points for a paper published in this journal. The paper in question begins from recalling (after the 2010 paper) main definitions and propositions of the formal theory of blocking power. Here are the titles of 9 sections which the paper consists of.
1. Introduction, or on politicians and mathematicians; 2. Three ways of theorizing on voting power; 3. The measurement of blocking power; 4. The blocking structure of a voting game; 5. Relational analysis of blocking power; 6. Relationships between three approaches to voting power; 7. A history of voting systems constructed for the EU Council of Ministers; 8. Blocking power in square root games; 9. Conclusions and a postscript. My aim in the second part (Sections 7-9) was to show that the third way of theorizing I proposed (it differs from naive theorizing of most politicians and commentators, as well as from the mainstream mathematical conceptualization and measurement of voting power) helps better understand the logic behind the historical process of constructing voting systems for the top body which has made decisions on behalf of the union of states with 6 members at its origin and now 28. The last section contains certain suggestions on how men and women of power who have the final say in devising voting rules for the EU could benefit from the expertise of men and women of knowledge who have worked out formal means to analyze intended or unintended consequences of the solutions chosen by the politicians. The postscript deals with how the accession of Croatia (1st July, 2013) affected blocking opportunities in the Nice voting game at the last stage of its use preceding its replacement (as of November 1, 2014) with the game defined by the Lisbon treaty. November 15, 2015 |